Produktuak Kategoria
- FM transmisorea
- 0-50w 50w-1000w 2kw-10kw 10kw +
- TV igorlea
- 0-50w 50-1kw 2kw-10kw
- FM antena
- telebista antena
- Antena Osagarriak
- Kable Connector Power Splitter Karga Dummy
- RF Transistor
- Energia hornidura
- Audio Ekipamenduak
- DTV Front End Ekipamendua
- Link System
- STL sistema Mikrouhin Link sistema
- FM irratia
- Power Meter
- Beste produktu batzuk
- Berezia Coronaviruserako
Produktuak Tags
fmuser Sites
- es.fmuser.net
- it.fmuser.net
- fr.fmuser.net
- de.fmuser.net
- af.fmuser.net -> afrikaansa
- sq.fmuser.net -> Albaniera
- ar.fmuser.net -> arabiera
- hy.fmuser.net -> Armenian
- az.fmuser.net -> azerbaijanera
- eu.fmuser.net -> euskara
- be.fmuser.net -> Bielorrusiera
- bg.fmuser.net -> Bulgarian
- ca.fmuser.net -> Katalana
- zh-CN.fmuser.net -> Txinera (sinplifikatua)
- zh-TW.fmuser.net -> Chinese (Traditional)
- hr.fmuser.net -> kroaziera
- cs.fmuser.net -> Txekiera
- da.fmuser.net -> Danimarkarra
- nl.fmuser.net -> Holandako
- et.fmuser.net -> Estoniera
- tl.fmuser.net -> Filipinoa
- fi.fmuser.net -> finlandiera
- fr.fmuser.net -> Frantsesa
- gl.fmuser.net -> Galiziera
- ka.fmuser.net -> Georgiarra
- de.fmuser.net -> alemana
- el.fmuser.net -> Greek
- ht.fmuser.net -> Haitiko kreolera
- iw.fmuser.net -> Hebreera
- hi.fmuser.net -> Hindi
- hu.fmuser.net -> Hungarian
- is.fmuser.net -> Islandiera
- id.fmuser.net -> Indonesiera
- ga.fmuser.net -> Irlandera
- it.fmuser.net -> Italian
- ja.fmuser.net -> Japoniera
- ko.fmuser.net -> Koreera
- lv.fmuser.net -> Letoniera
- lt.fmuser.net -> Lithuanian
- mk.fmuser.net -> mazedoniera
- ms.fmuser.net -> malaysiera
- mt.fmuser.net -> maltera
- no.fmuser.net -> Norwegian
- fa.fmuser.net -> persiera
- pl.fmuser.net -> poloniera
- pt.fmuser.net -> Portugesa
- ro.fmuser.net -> Romanian
- ru.fmuser.net -> errusiera
- sr.fmuser.net -> serbiera
- sk.fmuser.net -> Eslovakiera
- sl.fmuser.net -> Slovenian
- es.fmuser.net -> Gaztelania
- sw.fmuser.net -> Swahilia
- sv.fmuser.net -> Suediera
- th.fmuser.net -> Thai
- tr.fmuser.net -> Turkiera
- uk.fmuser.net -> ukrainera
- ur.fmuser.net -> urdua
- vi.fmuser.net -> Vietnamese
- cy.fmuser.net -> galesera
- yi.fmuser.net -> Yiddish
Potentzia eta anplitudea: Wattak, Tentsioak eta Erreferentziatutako Deibelak
Sarrera
Irrati maiztasuneko aplikazioetan (baina baita beste aplikazio askotan ere) oso ohikoa da seinale oso handiak eta oso txikiak jorratzea. Adibidez, errezeptore batek 100 W-ko potentzia igorri dezake eta 10 fW (edo 0.000'000'000'000'01 W) bakarrik jaso ditzake. Potentzia maila oso desberdinak zirkuitu berdinak partekatu ditzakete. Zifra horiek Wattetan adieraz daitezke ingeniaritza notazioa erabilita (goian bezala) edo notazio zientifikoa erabilita, 1 · 102 W eta 1 · 10 – 14 W bezala, baina nahiko zaila dira eta esponentea gaizki idatzita badago. , lortutako errorea itzela izango da.
Beste bide bat logaritmoa hartu eta dBm-en ahalmen guztiak bihurtzea da. 100 W bihurtu + 50 dBm eta 10 fW bihurtzen dira –110 dBm: zifra hauek askoz errazagoak dira bihotzetik idazteko eta idazteko. Ondoren, zirkuitu bloke desberdinen arintasuna eta etekina dBn adierazten bada ere, azken potentzia aurkitzeko, dena batu dezakegu elkarrekin biderkatu beharrean, kalkuluak are gehiago sinplifikatuz.
Mundu guztia ez dago eroso dB, dBm eta antzeko (pseudo) unitateekin: ez dago horiek erabiltzeko premia zorrotzarik, baina ingeniaritzan hain erabiliak daude, horiek saihesteko oso zaila da.
Teoria batzuk
Decibelak (dB) potentzia-erlazioak modu logaritmikoan adierazteko erabiltzen dira, beraz potentzia oso handiak eta oso txikiak zenbaki erosoak konparatu ahal izateko. Erabakia dimentsio gabeko sasi-unitatea da, bi botereen ratioak zehazten duelako. Hala ere, dezibeloak oso erabilgarriak direnez, dimentsio erlazio soil baten ordez egiazko boterea adierazteko, aipatutako dezibeloak oso maiz erabiltzen dira.
Potentziaz hitz egiten badugu, hurrengo ekuazioan W potentziako p dB-ren potentzia maila definitzen da p0 potentziari erreferentzia eginez:
10 faktorea da dezibelak "kanpai hamargarrenak" direlako. Bells-en egindako neurketarik ez dut sekula entzun, dezibeloak bakarrik erabiltzen dira.
Unitate ohikoena dBm da ("dBm") dBmW edo decibel-milliwatt bezala ere ezaguna da: dB-ko potentzia maila p0 = 1 mW-ren erreferentziarekin alderatuta. Batzuetan dBW ere erabiltzen da eta p0 = 1 W-rekin erlazionatutako potentzia-erlazioa adierazten dute, baina ez dira oso ohikoak.
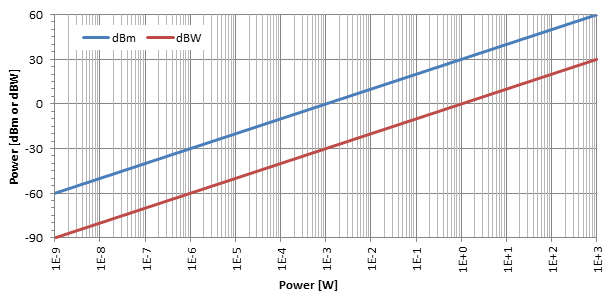
Goiko traman agerian denez, dezibelio bihurketaren eragin logaritmikoa nahiko nabaria da. Log-line trama honetan ikus daitekeenez, dBm eta dBW 30 dB-rekin bereizten diren bi lerro zuzen besterik ez dira: dBm dBW bihurtzea 30 besterik kendu behar da.
Zenbait domeinutan, telebistako harrera analogikoa bezala, ohikoa da tentsioa neurtzea indarraren ordez. Hau ez da arazoa inpedantzia ezagutzen eta konpontzen den bitartean (telebista-hartzaileek normalean 75 Ω erabiltzen dute).
Tentsio absolutuek dezibel eskala logaritmikoa ere aprobetxatu dezakete, dezibel mikrovolta (dBμV) eta dezibel boltsa (dBV) erabiliz. Ohikoena dBμV da u0 = 1 μV-rekin erlazionatutako tentsio-erlazioa adierazten duena. Batzuetan dBV ere erabiltzen da eta u0 = 1 V-rekin erlazionatutako tentsio erlazioa adierazten dute.
Kontuz tentsioek "20" erabiltzen dutela "10" ordez dB formulan. Hau da, dezibelak beti botere-razio gisa definitzen direlako; tentsioak bakarrik baditugu, lehenik eta behin karratuak jarri behar ditugu potentzia aurkitzeko. Bi logelaitismotik ateratako bi potentzia hori 10-ren lehendik dagoen faktorea 2-ren bidez biderkatuko da.
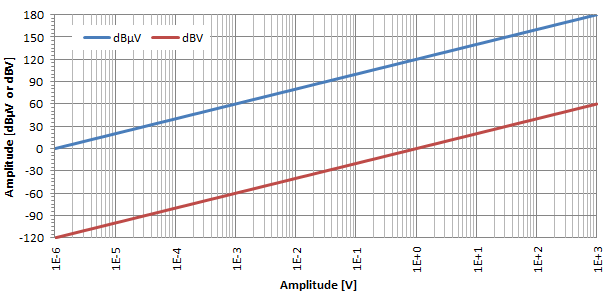
Aurreko irudian eta lehen bezala antzeman zen moduan, dezibelio bihurketaren eragin logaritmikoa nahiko nabaria da tentsioetan ere. Log-line trama honetan ikus daitekeenez, dBμV eta dBV 120 dB-rekin bereizten diren bi lerro zuzen besterik ez dira: dBμV dBV bihurtzea 120 besterik kendu behar da.
Orain, potentzia batetik tentsiora eta alderantziz bihurtu nahi badugu, inpedantzia ezagutu behar dugu. Ekuazio hau besterik ez dugu erabiltzen:
Bihurketa hau Zc inpedantzia erreala denean eta karga transmisio lerroarekin bat datorrenean bakarrik balio du.
Potentzia-maila dBm-n eta anplitudearen maila dBμV-n W-ren potentzia-funtzio gisa inplikatzen badugu, inpedantzia batengatik (hemen Zc = 50 Ω) honako hau lortuko dugu:
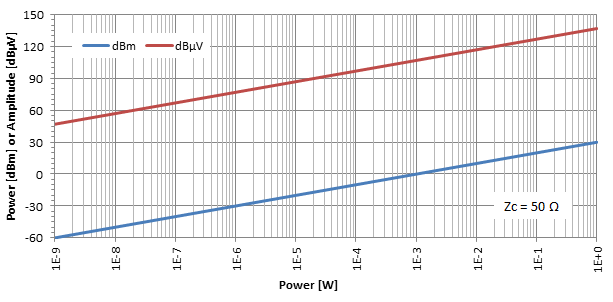
Arrazoi praktikoak
Lehen begiratuan, pentsa daiteke logaritmoa dela eta, poltsikoko kalkulagailua erabat beharrezkoa dela dBm-ri aurre egiteko. Egia esan, kalkulu zakarra zure buruan erraz egin daiteke. Hiru gertakari besterik ez dituzu gogoratu behar:
1 mW-ren potentzia 0 dBm da.
Energia bikoizten den bakoitzean, gehitu 3 dB.
Energia 10 faktore batekin handitzen den bakoitzean, gehitu 10 dB.
Orain, azter ditzagun adibide batzuk: demagun 26 dBm-ko potentzia maila dugula. 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB eta aurreko hiru adibide arruntekin erraz aurki dezakegu energia 1 mW · 10 · 10 · 2 · 2 = 400 .
Beste adibide bat: demagun -33dBm dugula: -33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB, eta 1 mW / 10 / 10 / 10 / 2 = 0.5 = XNUMX = XNUMX = XNUMX = XNUMX = XNUMX
Beste modu batean ere funtzionatzen du, adibidez 50 mW 1 mW · 10 · 10 / 2 besterik ez dira. DBm-en 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.
Horrek praktika batzuk eskatzen ditu baina oso erraza da. Ez da poltsikoko kalkulagailua bezain zehatza ± 2 dB-n bakarrik zehatza izan daitekeelako, baina, ahalegina dela eta, seinale baten indarraren oso ideia ona ematen du.
Antzeko metodo bat dBμV-rekin ere funtzionatzen du, baina arauak desberdinak dira:
1 µV-ren anplitudea 0 dBμV da.
Anplitudea bikoizten den bakoitzean, gehitu 6 dB.
Anplitudea 10 faktore batekin handitzen den bakoitzean, gehitu 20 dB.
Harrituta egon zaitezke aurretik erakutsitako kalkuluekin, non dB gehitzen zaion dBm-ri, nahiko arraroa baita. Hau da, dezibeloak sasi-unitateak direlako eta ez ohi duten moduan jokatzen. Bi potentziaren erlazioa dB-n adierazten da, baina dimentsio gabea da. Adibidez, 3 dB-k "bi aldiz" baino ez du esan nahi. DBm-n adierazitako potentzia benetan potentzia da: adibidez, 10 dBm-ek "10 aldiz 1 mW baino indartsuagoa" esan nahi du, hau da, 10 mW.
Orain, dezibelak (dB, dBm, ...) gehitzen dituzunean, haien izaera logaritmikoa dela eta, benetan jatorrizko irudiak elkarrekin biderkatzen ari zara. Beraz, 3 dB-ko irabazia 10 dBm-eko potentziari gehitzen baduzu, 13 dBm lortuko duzu. Baina benetan egin duzuna, 2 faktore bat biderkatzea 10 mW-ren potentziarekin 20 mW lortzen da, hau da, 13 dBm!
Orain arte hain ona, gehitzea askoz errazagoa da zure buruan egitea biderkatzea baino, eta horrek dezibelak hain erabilgarriak dira. Baina arazo bat dago: dezibelak batera gehitzea jatorrizko faktoreak biderkatzeari dagokioenez, nola gehitu daiteke bi seinaleen potentzia? Beno, ezin duzu. Ezin dBm gehitu dBm-era. Adibidez, 10 dBm (10 mW) seinalearen 13 dBm (20 mW) beste seinale baten potentzia uztartzen duen zirkuitu edo gailu bat baduzu, emaitza 10 mW + 20 mW = 30 da. mW 14.8 dBm da. Ez dago modu hori zuzenean dBm-n egiteko. Bi botereak Watt-en bihurtu behar dituzu, batu eta berriro bihurtu dBm-en. Hau dezibelioen muga handia da eta ohiko ezbeharra; zorionez, eragiketa hau ez da oso ohikoa.
Irrati kate bat eraiki nahi baduzu, igo FM irrati igorlea edo beste edozein behar duzu FM ekipoa, jar zaitez gurekin harremanetan jartzeko: [posta elektroniko bidez babestua].

